问题
- 索引是什么?
- 为什么选择用 B+ 树索引?
- 聚集索引和非聚集索引的区别?
- 为什么建议使用整型自增做主键?
简介
索引:是帮助 MySQL 高效获取数据的排好序的数据结构。
索引是应用程序设计和开发的一个重要方面,若索引太多,应用程序的性能可能会受到影响。而索引太少,对查询性能又会产生影响。需要找到一个合适的平衡点,这对应用程序的性能至关重要。
InnoDB 存储引擎支持 3 种常见的索引:
- B+ 树索引
- 全文索引
- 哈希索引
InnoDB 存储引擎索引
B+ 树索引
注意:B+ 树中的 B 不是代表二叉(binary),而是代表平衡(balance),因为 B+ 树是从最早的平衡二叉树演化而来,但是 B+ 树不是一个二叉树。
B+ 树索引并不能找到一个给定键值的具体行,B+ 树索引能找到的只是被查找数据行所在的页,然后数据库通过把页读入到内存,再在内存中进行查找,最后得到要查找的数据。
MyISAM:索引文件和数据文件是分离的,非聚集索引。
InnoDB
1 | // MyISAM存储引擎,存储在*.MYI |
聚集索引:叶子节点包含了完整的数据记录。
非聚集索引:索引文件和数据文件没有聚集在一起。
主键索引
二级索引
全文索引
哈希索引
数据库的索引一般在磁盘上,数据量大的情况可能无法一次装入内存,B+ 树的设计可以允许数据分批加载,同时树的高度较低,提高查询效率。
为什么 MySQL 选择用 B+ 树索引?
当数据在磁盘中时,磁盘 IO 会成为最大的性能瓶颈,设计的目标应该是尽量减少 IO 次数;而树的高度越高,增删改查所需要的 IO 次数也越多,会严重影响性能。树的查找性能取决于树的高度,让树尽量平衡,就是为了降低树的高度。
二叉树
二叉查找树
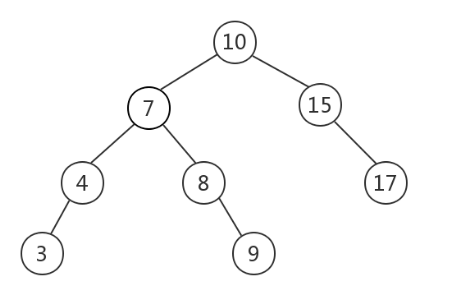
- 对于树中的任意一个节点,左子树节点比根节点小,右子树节点比根节点大。
- 时间复杂度:O(logn)
- 缺点:不平衡,极端情况如有序序列,二叉排序树退化成链表,时间复杂度变为 O(n)。

平衡二叉树(AVL)
- AVL 树是严格的平衡二叉树,所有节点的左右子树高度差不能超过 1。
- AVL 树查找、插入和删除在平均和最坏情况下都是 O(logn)。
- 缺点:旋转耗时,AVL 树在删除数据时效率很低,量级为 O(logn)。
红黑树

- 与 AVL 树相比,红黑树并不追求严格的平衡,而是大致的平衡。
- 红黑树引入了颜色,当插入或删除数据时,只需要进行 O(1) 次数的旋转以及变色就能保证基本的平衡。
- 缺点:树的高度太高。
B 树

B 树是一种多路搜索树,它的每个节点可以拥有多于两个孩子节点,M 路的 B 树最多能拥有 M 个孩子节点。
- 不再是二叉查找,而是 M 叉查找,树的高度能够大大降低。
- 叶子节点,非叶子节点,都存储数据。
- 中序遍历,可以获得所有节点。
B+ 树
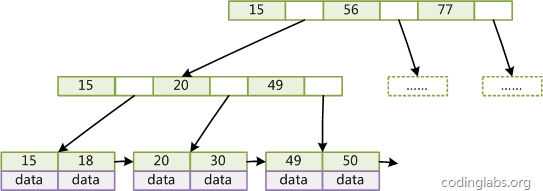
B+ 树是在 B 树的基础上进行改造:
- 非叶子节点不再存储数据,数据只存储在同一层的叶子节点上。
- 叶子之间,增加了链表,获取所有节点,不再需要中序遍历。
- 优点:在查询多条数据或范围查询时,B 树可能要跨层访问,而 B+ 树数据都在叶子节点,不用跨层,同时由于有链表结构,只需要找到首尾,就能把所有数据取出来。
局部性原理与磁盘预读
- 磁盘预读:磁盘读写并不是按需读取,而是按页预读,一次会读一页的数据,每次加载更多的数据,如果未来要读取的数据就在这一页中,可以避免未来的磁盘 IO,提高效率(通常,一页数据是 4K)。
- 局部性原理:软件设计要尽量遵循“数据读取集中”与使用到一个数据,大概率会使用其附近的数据,这样磁盘预读能充分提高磁盘 IO。
总结
1) 二叉查找树 (BST):解决了排序的基本问题,但是由于无法保证平衡,可能退化为链表。
2) 平衡二叉树 (AVL):通过旋转解决了平衡的问题,但是旋转操作效率太低。
3) 红黑树:通过舍弃严格的平衡和引入红黑节点,解决了 AVL 旋转效率过低的问题,但是在磁盘等场景下,树仍然太高,IO 次数太多。
4) B 树:通过将二叉树改为多路平衡查找树,解决了树过高的问题。
5) B+ 树:在 B 树的基础上,将非叶节点改造为不存储数据的纯索引节点,进一步降低了树的高度,此外将叶节点使用指针连接成链表,范围查询更加高效。